物理定律的对称性和宇称不守恒
·沈觉宏整理编辑·
宇称守恒与宇称不守恒的讨论
§3.7 物理定律的对称性和宇称不守恒
文章内容选编于李政道杨振宁先生作品,作者仅做整编,整编作者以刮号区别。
( Parity Nonconservation)
1,对称性和守恒定律
2,空间反演不变性和宇称守恒
3,弱作用宇称不守恒问题
4, PC联合变换对称性和CPT定律
5, 弱相互作用和生物手性(Chirality)
[说句笑话,所谓运动?就是不不守恒,尽管运动可以有对称性,比如左旋100次,右旋100次。但是既然有运动就必定要打破对称性。同时,物质在运动中左右对称也不是绝对的,在自然界左旋运动的物质占有绝对优胜地位。]



1,对称性和守恒定律
对称性-----物体的状态在一定的变换下具有的不变性。
艺术中的对称性(骑士图)
文学中的对称性:
上海自来水来自海上
南山长生松生长山南
物理规律的对称性----物理规律在一定变换下的不变性。就是某种物理状态或过程在一定的变换下
(例如转动、平移等等),它所服从的物理规律不变。
物理规律的对称性的重要性:
· 在探索未知的物理规律的时候,可以以普遍的对称性作为指引;
· 物理规律的每一种对称性(即不变性)通常都相应于一种守恒定律。
空间平移不变性………………动量守恒
空间转动不变性………………角动量守恒
时间平移不变性………………能量守恒
空间反演不变性………………宇称守恒
第一类规范不变性……………电荷守恒
2,空间反演不变性和宇称守恒
(1) 空间反演不变性
空间反演: r -r,
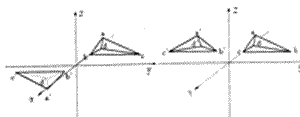
空间反演实质上和
镜象变换等价。
镜象变换把左手变
成右手, 左? ? 右
对称。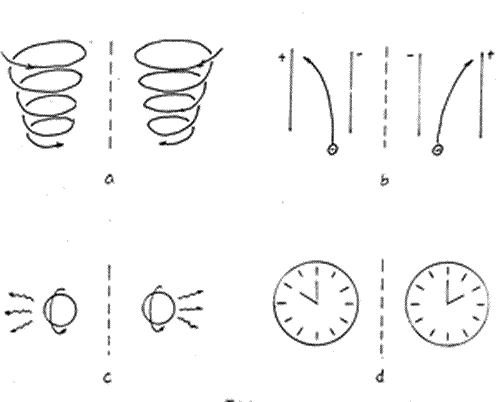
左右对称的两个状态或两种过程在自然界中都同样能够存在或发生,它们都服从同样的物理规律。
尽管在镜象变换下,物理过程的状态变化了,但它们服从的物理规律却没有变,这就是物理规
律的空间反演不变性。
f = ma -f = -ma
量子力学: 空间反演不变性 宇称守恒
(2) 宇称守恒
对于微观粒子:
一种运动状态: ψ(x,y,z)
相应的镜象状态: ψ(? x,? y,? z)空间反演时规律不变
|ψ(x,y,z)|2 =|ψ(? x,-y,-z)|2
由此可得:
ψ(x,y,z)=±ψ(-x,-y,-z)
若 ψ(x,y,z)=+ψ(-x,-y,-z)
偶宇称,用π=+1表示若 ψ(x,y,z)=-ψ(-x,-y,-z)
奇宇称,用π=? 1表示量子力学:
空间反演算符 P : r ? - r p ? - p
L = r ? p
P : L ? L J ? J
对波函数 P? (r) = ? (-r) Pf(r)g(r)=f(-r)g(-r)
原状态: ? (r) 空间反演态:? (-r)
? (r)满足: ![]()
![]()
![]() 如果? (-r)也满足:
如果? (-r)也满足:
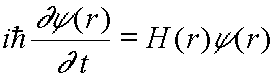
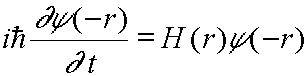
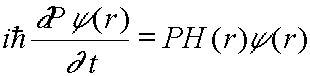
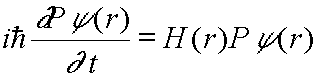
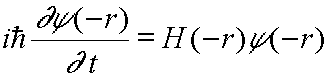
即要 PH = HP
![]() 空间反演不变 H和P对易,有共同本征函数
空间反演不变 H和P对易,有共同本征函数
H? (r)=E? (r)
PH? (r)=PE? (r)=EP? (r)
由 PH = HP HP? (r)=EP? (r)
? (r) 和P? (r)满足同一方程,对应于同一本征值
? (r) 和P? (r) 描述同一物理状态
P? (r)=? ? (r)
? (r)=P2? (r)=? P? (r)=? 2 ? (r)
? 2=1 ? = 1 P的本征值为 1
P? (r)=? (-r)= ? (r)
P和H对易 宇称是守恒量 只要微观粒子的运动规律具有空间反演不变性(实质上是代表相互作
用能量的哈密顿算符在空间反演变换下不变),则微观粒子体系具有确定的宇称,且保持不变。
如果一个孤立体系具有偶宇称,则永远是偶宇称,如果具有奇宇称,则永远是奇宇称? ? 宇称
守恒定律。
·偶宇称和奇宇称
·体系的总宇称和部分宇称
例如反应:
a+b→c+d
反应前的波函数为:
? i=? a ? b ? r
? a,? b为粒子或原子核内部状态的波函数
? r 则为它们相对运动状态的波函数 反应前体系的宇称为
? i=? a ? b ? r
如果a和b的相互作用是中心力,它们相对运动的轨道角动量量子数为 ? ,则相应的波函数就是球
谐函数
Y? m=P? ? m? (cos? )eim? r ? ? r : r ? r ? ? ? ? ? ? ? ? + ?
Y? m (? r) = (? 1) ? Y? m (r)
即相对运动波函数的宇称 ? r=(? 1) ?
? = 0 1 2 3
? r=+1 -1 +1 -1
这样就有
? i=? a ? b (? 1) ?
如果反应后c和d的相对运动轨道角动量为 ? ’
则反应后体系的宇称为
? f=? c ? d (? 1) ? ’
宇称守恒就要求
? a ? b (? 1) ? = ? c ? d (? 1) ? ’(3) 粒子的内禀宇称及宇称守恒定律的应用
1) 粒子的内禀宇称
每一种粒子都应具有一种确定的宇称值,这宇称又称为粒子的内禀宇称或本征宇称。
只能测 ? (r)? 2
规定: ? p=? n=? ? =+1
利用它们参加的反应和宇称守恒定律,就可确定别的粒子的宇称
π介子 ? + , ? - , ? 0 : ? =-1
2) 偶-偶核基态的宇称
由 ? p=? n=+1
可以确定偶-偶核基态的宇称也是偶宇称
? =(-1) ? (-1) ? =(-1) 2? =+1
偶-偶核基态的自旋 J=0,
对偶-偶核的基态,J? =0+。
3) 由宇称守恒定律确定原子核激发态的宇称
通过原子核的α衰变确定子核激发态宇称
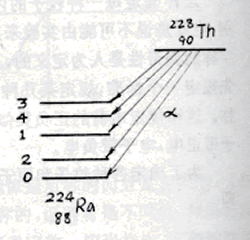 Th228? Ra224+He4
Th228? Ra224+He4
0+ J ? 0+
激发态的自旋为J角动量守恒: J=-L J=?
? i=+1 ? f=? Ra ? He (-1)?
=? Ra (-1)J=+1
? Ra= (-1)J J? =0+, 1 - , 2+ ,··
即J为奇数的激发能级宇称为-1,J为偶数的则为+1
4) 原子偶极跃迁的宇称选择原则
3,弱作用宇称不守恒问题
(1) θ-τ疑难
1956年公布的结果表明它们的质量和寿命惊人的一致
θ+→π++? 0m=(966.7? 2)meτ=(1.21? 0.02)10-8s
τ+→π++π-+π+ m=(966.3? 2)me τ=(1.19? 0.05)10-8 s
宇称: π介子的自旋和宇称为 0-
τ+→π++π-+π+
J=0 ? = 0 ? =(-1)(-1)(-1)(-1)0=-1
τ+:J? =0 -
θ+→π++? 0
J = ? ? =(-1)(-1)(-1)? =(-1) ?
θ+: J? =0 +, 1-, 2 +, 3 -
如果θ+和τ+是同一种粒子,只是有两种不同的衰变方式,则应当具有同一种自旋和宇称,如果自旋
为零则按两种衰变方式确定的宇称相反。
(2) 李政道—扬振宁假说
T.D.Lee and C.N.Yang, Phys Rev 104, 254(1956)
李政道和杨振宁在θ-τ疑难的启发下,大胆地提出了弱相互作用过程中宇称不守恒的假说,并具体建议在原子核的β衰变和基本粒子衰变中可以通过哪些实验来检验宇称是否守恒 很多人反对 郎道 泡利
(3) 极化Co60 衰变实验
Co60 ? Ni60 + e- + ?
C.W.Wu et al., Phys.Rev., 105,1413(1957)
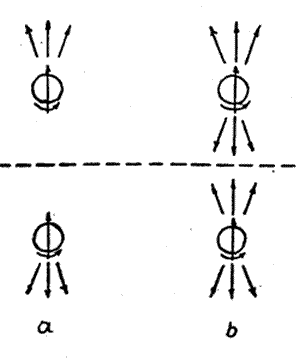
后来的实验也证明,在介子衰变过程中宇称也是不守恒的,这样宇称守恒定律就被证明在整个弱相互作用中都是不成立的了。
正如爱因斯坦所说:“一个矛盾的实验结果就足以
推翻一种理论。”实验是最有权威性的。
他们的杰出工作获得了1957年的诺贝尔物理学奖。
4, PC联合变换对称性和CPT定律
杨振宁、李政道 朗道 萨拉姆:
1957 “二分量中微子理论”。
中微子都是左旋的,不存在右旋中微子,而反中微
子则都是右旋的,不存在左旋反中微子,这样,空间反演对称性在中微子身上就遭到的彻底的破坏!
二分量中微子理论很快得到了实验的证实。
空间反演变
用字母P表示
C表示电荷共轭(音:饿)变换
正反粒子互换
T表示时间反演变换
把时间颠倒 ,将t变成-t。
过去认为:
P、C、T三种独立变换下物理规律都是不变的
只有左旋中微子和右旋的反中微子这一事实,不仅破坏了空间反演不变性也破坏了电荷共轭变换
不变性,因为在电荷共轭变换下:左旋中微子
左旋的反中微子 不存在
大家认为PC联合变换对称性仍然有效。
1964年,克罗宁(J.W.Cronin)和菲奇(V.L.Fitch)等人通过实验发现:
长寿命K°介子的衰变中,PC变换的对称性有轻度的破坏,破坏程度为千分之二左右。(3.27)
CPT联合变换:
物理规律在CPT联合变换下是严格保持不变的
PC变换的对称性破坏 T不变性破坏。
到目前为止还没有在其它情况下发现T不变性遭到破坏的证据。
我们的物理世界在总体上看来是非常对称的,为什么在这个对称的世界中会失去某些对称性这是一个令人非常困惑的问题。
5. 弱相互作用和生物手性(Chirality)
物理学: 生物学:
研究最简单的问题 研究最复杂的系统
喜欢问Why? 原因 What for? 目的
研究大概率事件 研究小概率事件
两者有联系
氨基酸有左旋、右旋两种,化学性质一样
H H
NH3 C C NH3
CH3 COOH COOH CH3
L-Ala D-Ala
生物活体中的氨基酸都是L性,
核苷酸的糖环都是D性
15万种生物,每种几万种蛋白质,由8种核苷酸20种氨基酸构成
生物手性的起源?
不对称力(弱相互作用)产生?影响多大?
择优选择?
实验:? 衰变极化电子轰击L和D性氨基酸,反应速
率差10 - 6, 浓度差10 - 2
主要原因可能是化学动力学
[事实结果证明,中微子都是左旋的,不存在右旋中微子,而反中微子则都是右旋的,不存在左旋反中微子。这样,空间反演对称性在中微子身上就遭到了彻底的破坏!并且,物质运动偏重左旋。左旋物质和左旋运动将成为自然界不可抗拒的主旋律!人类,为什么不去遵循自然界的主旋律呢?违背自然规律的严重后果是什么将不言自明!中微子的特点,速度之快,无法捕捉,变化之快。 -- 沈觉宏 2000年 ]
联系左旋 联系我们 请关注左旋
|
在海洋中“窃窃私语”的中微子 《科学时报》 主办:中国科学院办公厅 承办:科学时报社
日美联合研究小组发现新型中微子 记者 何德功
太阳中微子之谜
日美中科学家揭开“太阳中微子丢失”之谜
中微子的總質量
中 微 子 的 質 量
科 學 家 發 現 中 微 子 有
質 量
偵 測 高 能 量 的
中 微 子
太阳中微子之谜
“上帝是个用惯左手的弱者”
<上帝是“左撇子”吗?>
李政道话当年:我给毛主席演示对称
返回左旋理论文章精选>>>>>
物理规律的对称性和宇称不守恒与共产主义运动有什么关系?》有待探索
右派为什么如此嫉恨左旋?》有待探索
自然规律是不以人的意志为转移的,预示了什么问题?》有待探索
不打棍子不扣帽子,请hq等朋友探讨,一个不可忽视的信息技术之迷?...[从红五星来]
请沈觉宏用理论反驳.[hq] 2003.
告戒zwl老朱,马恩列斯毛五大救星不能随便骂的[小玉]
科学告诉我们:地球是向右转的,她不仅自转是向右的,而且她与其他的 行星一道围绕太阳向右公转......而且,银河系也是向右转的,总星系也是如此------由此可见,向右旋转才是人间及宇宙间的客观的、必然的规律。所以,左旋是邪道,右旋才是真理!-- [中国右派联盟]2002.
【左旋于1999年建立网站,公开左旋理论和一系列方法以后,立即遭遇激烈的论战。很多人以相对论抨击左旋,认为事物都是对称的,认为偏向左旋的论述,是站不住脚跟的。直到如今,依然有人继续质疑,甚至上门论战。
左旋把科学分为二大类:合符客观规律和违背客观规律,前者天长地久,后者早晚解体消失。 左旋理论频道自网站诞生同时设立,有许多有意义的文章,也是左旋战胜各种挑战,得以立足的基地。上文由沈先生2000年编辑,发挥了重要作用。---左旋理论研究】
--------------------------------------------------------------------------------
返回左旋理论文章精选》》》

